Divergence
Divergence is an operation on a vector field that tells us how the field behaves toward or away from a point. Locally, the divergence of a vector field $\vec{F}$ in $\mathbb{R}^2$ or $\mathbb{R}^3$ at a particular point $P$ is a measure of the “outflowing-ness” of the vector field at $P$.
If $\vec{F}$ represents the velocity of a fluid, then the divergence of $\vec{F}$ at $P$ measures the net rate of change with respect to time of the amount of fluid flowing away from $P$ (the tendency of the fluid to flow “out of” P). In particular, if the amount of fluid flowing into $P$ is the same as the amount flowing out, then the divergence at $P$ is zero.
Definition: divergence in $\mathbb{R}^3$
If $\vec{F} = \langle P,Q,R \rangle$ is a vector field in $\mathbb{R}^3$ and $P_x, , Q_y,$ and $R_z$ all exist, then the divergence of $\vec{F}$ is defined by
$$\begin{aligned}
\operatorname{div} F &=P_{x}+Q_{y}+R_{z} \
&=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}
\end{aligned}$$
Note the divergence of a vector field is not a vector field, but a scalar function. In terms of the gradient operator
$$\vec{\nabla}=\left\langle\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right\rangle$$
divergence can be written symbolically as the dot product
$$\operatorname{div} \vec{F}=\vec{\nabla} \cdot \vec{F}.$$
Note this is merely helpful notation, because the dot product of a vector of operators and a vector of functions is not meaningfully defined given our current definition of dot product.
If $\vec{F} = \langle P,Q \rangle$ is a vector field in $\mathbb{R}^2$ , and $P_{x}$ and $Q_{y}$ both exist, then the divergence of $\vec{F}$ is defined similarly as
$$\begin{aligned}
\operatorname{div} \vec{F} &=P_{x}+Q_{y} \
&=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y} \
&=\vec{\nabla} \cdot \vec{F}
\end{aligned}.$$
To illustrate this point, consider the two vector fields in Figure 1. At any particular point, the amount flowing in is the same as the amount flowing out, so at every point the “outflowing-ness” of the field is zero. Therefore, we expect the divergence of both fields to be zero, and this is indeed the case, as
$$\text{div}(\langle 1,2 \rangle ) = \dfrac{\partial}{\partial x} (1) + \dfrac{\partial}{\partial y}(2) = 0$$
and
$$\text{div}(\langle -y,x \rangle ) = \dfrac{\partial}{\partial x} (-y) + \dfrac{\partial}{\partial y} (x) = 0.$$
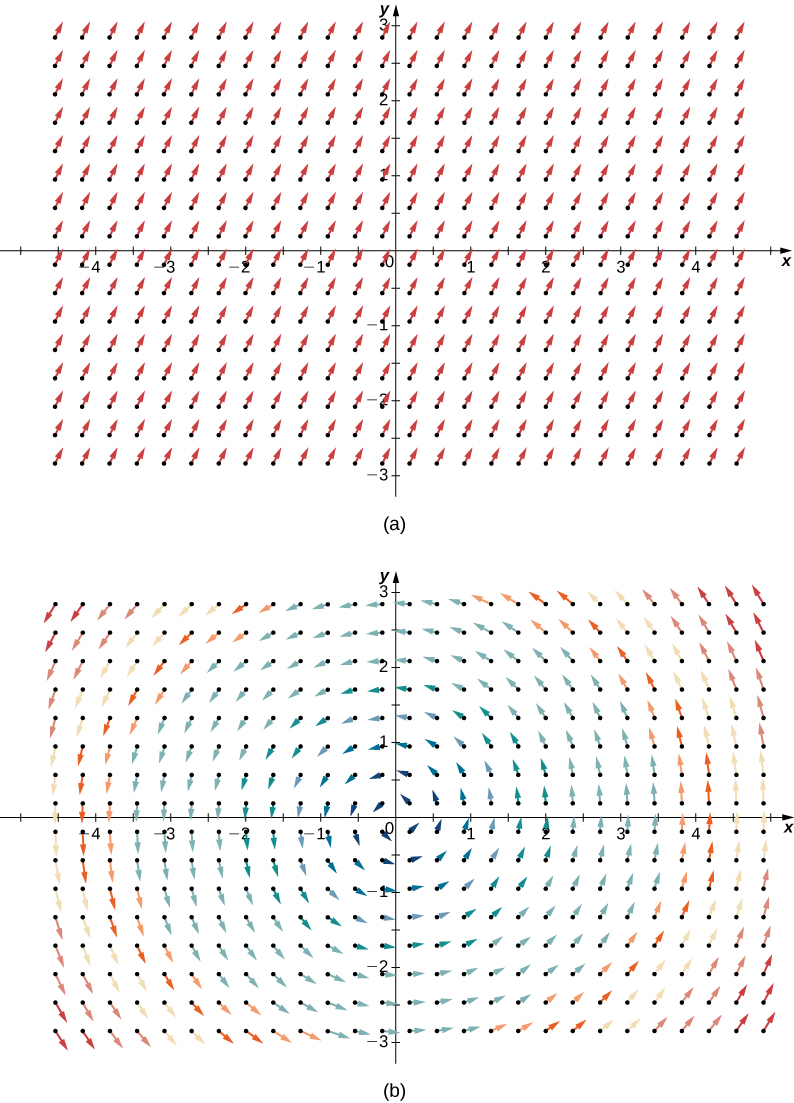
Figure 1: (a) Vector field ⟨1, 2⟩ has zero divergence. (b) Vector field ⟨−𝑦, 𝑥⟩ also has zero divergence.
By contrast, consider radial vector field $\vec{R}(x, y)=\langle-x,-y\rangle$ in Figure 2. At any given point, more fluid is flowing in than is flowing out, and therefore the “outgoingness” of the field is negative. We expect the divergence of this field to be negative, and this is indeed the case, as
$$\operatorname{div}(\vec{R})=\frac{\partial}{\partial x}(-x)+\frac{\partial}{\partial y}(-y)=-2$$
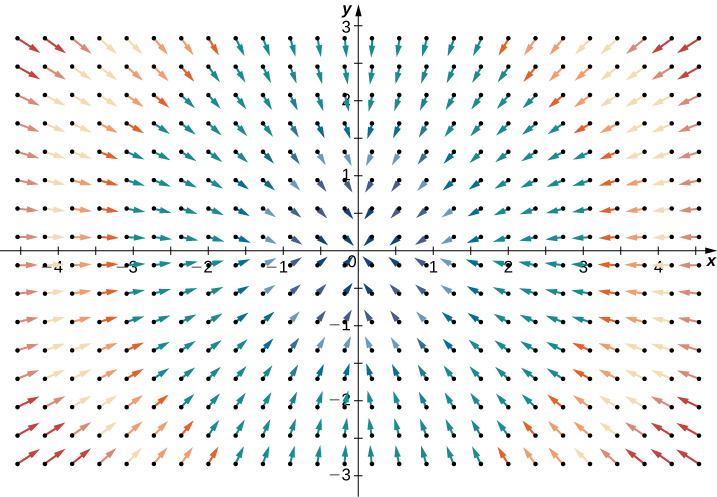
Figure 2: This vector field has negative divergence.
To get a global sense of what divergence is telling us, suppose that a vector field in $\mathbb{R}^2$ represents the velocity of a fluid. Imagine taking an elastic circle (a circle with a shape that can be changed by the vector field) and dropping it into a fluid. If the circle maintains its exact area as it flows through the fluid, then the divergence is zero. This would occur for both vector fields in Figure 1. On the other hand, if the circle’s shape is distorted so that its area shrinks or expands, then the divergence is not zero. Imagine dropping such an elastic circle into the radial vector field in Figure 2 so that the center of the circle lands at point (3, 3). The circle would flow toward the origin, and as it did so the front of the circle would travel more slowly than the back, causing the circle to “scrunch” and lose area. This is how you can see a negative divergence.
Curl
The second operation on a vector field that we examine is the curl, which measures the extent of rotation of the field about a point. Suppose that $\vec{F}$ represents the velocity field of a fluid. Then, the curl of $\vec{F}$ at point $P$ is a vector that measures the tendency of particles near $P$ to rotate about the axis that points in the direction of this vector. The magnitude of the curl vector at $P$ measures how quickly the particles rotate around this axis. In other words, the curl at a point is a measure of the vector field’s “spin” at that point. Visually, imagine placing a paddlewheel into a fluid at $P$ , with the axis of the paddlewheel aligned with the curl vector (Figure 3). The curl measures the tendency of the paddlewheel to rotate.
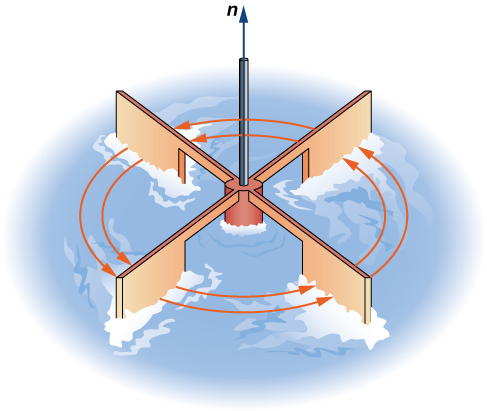
Figure 3: To visualize curl at a point, imagine placing a small paddlewheel into the vector field at a point.
Consider the vector fields in Figure 1. In part (a), the vector field is constant and there is no spin at any point. Therefore, we expect the curl of the field to be zero, and this is indeed the case. Part (b) shows a rotational field, so the field has spin. In particular, if you place a paddlewheel into a field at any point so that the axis of the wheel is perpendicular to a plane, the wheel rotates counterclockwise. Therefore, we expect the curl of the field to be nonzero, and this is indeed the case (the curl is $2,\mathbf{\hat k}$).
To see what curl is measuring globally, imagine dropping a leaf into the fluid. As the leaf moves along with the fluid flow, the curl measures the tendency of the leaf to rotate. If the curl is zero, then the leaf doesn’t rotate as it moves through the fluid.
Definition: Curl
If $\vec{F} = \langle P,Q,R \rangle$ is a vector field in $\mathbb{R}^3$ and $P_x, , Q_y,$ and $R_z$ all exist, then the curl of $\vec{F}$ is defined by
$$\begin{aligned}
\operatorname{curl} \vec{F} &=\left(\boldsymbol{R}{y}-Q{z}\right) \hat{\mathbf{i}}+\left(\boldsymbol{P}{z}-\boldsymbol{R}{x}\right) \hat{\mathbf{j}}+\left(Q_{x}-\boldsymbol{P}_{y}\right) \hat{\mathbf{k}} \
&=\left(\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{y}}-\frac{\partial Q}{\partial z}\right) \hat{\mathbf{i}}+\left(\frac{\partial \boldsymbol{P}}{\partial z}-\frac{\partial \boldsymbol{R}}{\partial x}\right) \hat{\mathbf{j}}+\left(\frac{\partial Q}{\partial x}-\frac{\partial \boldsymbol{P}}{\partial y}\right) \hat{\mathbf{k}}
\end{aligned}$$
Note that the curl of a vector field is a vector field, in contrast to divergence.
The definition of curl can be difficult to remember. To help with remembering, we use the notation $\vec{\nabla} \times \vec{F}$ to stand for a “determinant” that gives the curl formula:
$$\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \
\frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \
P & Q & R
\end{array}\right|.$$
The determinant of this matrix is
$$\left(R_{y}-Q_{z}\right) \hat{\mathbf{i}}-\left(R_{x}-P_{z}\right) \hat{\mathbf{j}}+\left(Q_{x}-P_{y}\right) \hat{\mathbf{k}}=\left(R_{y}-Q_{z}\right) \hat{\mathbf{i}}+\left(P_{z}-R_{x}\right) \hat{\mathbf{j}}+\left(Q_{x}-P_{y}\right) \hat{\mathbf{k}}=\operatorname{curl} \vec{F}.$$
Thus, this matrix is a way to help remember the formula for curl. Keep in mind, though, that the word determinant is used very loosely. A determinant is not really defined on a matrix with entries that are three vectors, three operators, and three functions.
If $\vec{F} = \langle P,Q \rangle$ is a vector field in $\mathbb{R}^2$ , then the curl of $\vec{F}$ , by definition, is
$$\operatorname{curl} \vec{F}=\left(Q_{x}-P_{y}\right) \hat{\mathbf{k}}=\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) \hat{\mathbf{k}}$$